Covalent bonds are composed of electron pairs, for reasons that we will go into in more detail later on. A bond formed from one pair of electrons is a single bond, one from two pairs of electrons a double bond, and one from three pairs a triple bond.
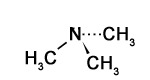
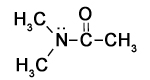
The figure to the right shows three representations of the simple molecules methane and water:
The first is a Lewis representation that shows the connectivity of the molecules - which atom is bound to which - but doesn’t make any attempt to represent the shape accurately.
The 'ball and stick' model shows the atoms as balls and the bonds between them as sticks, and makes a stab at accurately describing the geometric relationship between nuclei. But of course, both the 'balls' and the 'sticks' are just regions where there is a high probability of finding the electrons associated with the molecule.
A more accurate representation is the space-filling model, showing some surface within which electron density is high. This, too, is a representation: molecules are not like masses of peanuts stuck together with chocolate. In reality the functions that describe where we find the electrons of the molecule have non-zero values at every point in the universe except for certain surfaces called nodes, and the selection of where we draw the 'edge' of the molecule is completely arbitrary. We will go into this in more detail in the chapters that follow.
Covalent bonding is not restricted to the tiny lumps of matter we are used to calling molecules. In diamond, a single solid lump of matter big enough to see - though rarely as large as a hen’s egg - is linked together by covalent bonds in a giant covalent structure.

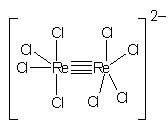
The limitation to single, double, and triple bonds arises from the number of bonding electrons present in atoms and how they are arranged in space. Between d-block atoms with many bonding electrons, a few compounds with quadruple bonds have been reported.
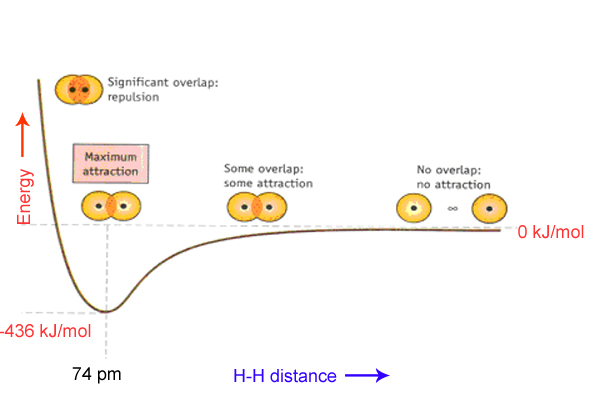
Bond energies are defined by separating the molecule into its component atoms and dividing the energy needed to do this between the number of bonds that are broken. This is straightforward for methane, where all the bonds are C-H bonds, or water, where all the bonds are O-H bonds. For more complicated cases comparison of results for a range of similar compounds and a bit of algebra might and be required to determine bond energies. Or might have been, it would be better to say: fortunately all C-H bonds and all O-H bonds are pretty much the same, no matter what molecule they are found in, and nowadays you would look up the bond energy of a 'C-H' bond in a table based on experiments other people have done before. You will find there can be quite a bit of variation in the bond energies quoted from different sources, as they have been calculated from different sets of experimental data. Typical covalent single bonds have energies between 150 kJ.mol–1 and 500 kJ.mol–1, while multiple bonds are stronger; the C=C bond energy is about 600 kJ.mol–1 and the triple bond in N2 is about 950 kJ.mol–1.
Ionic
A purely covalent bond has the electrons that form the bond equally attracted to both nuclei. This ideal case will only ever be achieved if the nuclei are of the same element and in exactly the same environment - thus the bond in molecular nitrogen, N2, the carbon-carbon bond in ethane, CH3CH3, and the O-O bond in hydrogen peroxide, HOOH, can all be considered purely covalent in nature. If the electrons that form the bond are more strongly attracted to one nucleus than another, putting an arbitrary surface between the nuclei will give a region of positive charge and a region of negative charge on the other. The material can then be considered as a three-dimensional array of positive and negative ions. The more a substance approaches to ‘ideal’ ionic bonding, the less localised the bonds can be considered to be, with each ion interacting with many other ions of the same and opposite charge.
![[Figure 1.3 adaptation] [I think it would be cool if you could mouse-over to toggle between two versions of the figure]](ch1_p3_5.jpg)
The structure of a crystal of sodium chloride, NaCl, consists of the network shown repeated many gazillion times in all directions. The positive sodium ions, Na+, and the negative chloride ions, Cl-, adopt this geometry in order to maximise attractive interactions and minimise repulsive ones. Note that the lines drawn are just there to make the structure look three-dimensional: unlike the lines in a ball-and-stick representation of a covalently-bound molecule, they do not correspond to regions of increased electron density.
Instead of bond energy, we talk about the lattice energy for an ionic material. This is the energy required to take one mole of the substance and separate all the ions until they are an infinite distance apart. Typical lattice energies are higher than covalent bond energies, and depend strongly on the charge of the ions- as we would expect from Coulomb’s Law.
For example:
NaCl, ELattice = 790 kJ.mol–1 q1 = q2 = 1
MgF2, ELattice = 2905 kJ.mol–1 q1 = 2, q2 = 1
MgO, ELattice = 2905 kJ.mol–1 q1 = q2 = 2
Metallic
In the third form of bonding, the most loosely bound electrons in an atom can minimise their energy not by migrating to another atom as in ionic bonding, or by sitting happily in a fixed bond between two nuclei, but by migrating freely throughout the material interacting with as many nuclei as possible. These freely moving electrons provide the negative charge that holds the positively charged metal centres (nuclei + core electrons) together.
For metals, we cannot define a specific bond energy, so like ionic solids we measure the strength of bonding in terms of how much energy is needed to separate all the atoms in the solid until they are not interacting with each other- the vaporisation energy. This more or less increases with the number of electrons in the outer shell of the atom.
For example:
Na, EVap = 100 kJ.mol–1, 1 valence electron
Al, EVap = 330 kJ.mol–1, 3 valence electrons
W, EVap = 849 kJ.mol–1, 6 valence electron
Dispersion Interactions
Ions may attract or repel one another. But what about substances where the charges are balanced? Once we have covalent bonding to give rise to an uncharged molecule, how will it interact with other molecules? It turns out there is always an attractive force between uncharged molecules. This is because electrons never sit still.
Imagine a molecule with a uniform distribution of electric charge throughout the molecule - for example, N2, or CH4, or C60. This uniform distribution is actually an average, and from one instant to another the electric charge will not be uniform: one part of the molecule will be more negative, and another part will be more positive. Hence, a molecule nominally without a dipole will actually have one, it will just be randomly oriented from one instant to the next.
![[Adaptations of Figures 1.4 and 1.5]](ch1_p3_6.jpg)
If we have more than one of these molecules, Coulomb’s law tells us that they will tend to align so that their bits with the same charge keep away from one another and their bits with the opposite charge are close together. Once they are aligned like this, the interaction between the molecules will tend to reinforce the temporary dipoles that arose originally from the random movements of the electrons.
![[Adaptations of Figures 1.4 and 1.5]](ch1_p3_7.jpg)
This net attractive force, which we call an induced dipole-induced dipole force, is found between all covalent substances. Because the movements of electrons are very rapid compared with the movements of molecules, the induced dipoles are always oriented so that their interaction is favourable.
The main factor determining the strength of this favourable interaction is how free the electrons are to move about the molecule- its polarisability. Where electrons are held relatively loosely, they can be induced to form a larger dipole and give stronger induced dipole-induced dipole interactions than where they are held strongly. Usually, the larger an atom is, the more polarisable are the electrons associated with it. Fluorine is one of the smaller atoms, and forms very strong bonds with many other elements in which the electrons are tightly bound: thus, forces between molecules containing chlorine are often quite weak and many compounds of quite high molecular mass containing fluorine are gases at room temperature - for example, SF6 and PF5. Uranium hexafluoride, despite its high molecular mass, sublimes at 57°C.
Counterintuitively, if a compound has a permanent dipole, the interactions between its molecules are not much stronger than those arising from temporary dipoles – at least in the gas and liquid phases. This is because the random thermal motions that keep tumbling the molecules about will sometimes bring the dipoles together in an attractive way, but sometimes in a repulsive way: because the dipole is a permanent part of the molecule, it cannot change in response to conditions and the dipole-dipole force between molecules are not always attractive.
The size of the dispersion force generally increases with molecular weight, and can be estimated from the energy of vaporisation of a molecular substance.
For example,
Butane, C4H10, EVap = 24 kJ.mol–1
Octane, C8H18, EVap = 42 kJ.mol–1
Dodecane, C12H26, EVap = 61 kJ.mol–1
Hexadecane, C16H34, EVap = 81 kJ.mol–1
Hydrogen Bonding
Permanent dipoles will be able to give strong bonding between molecules if they are strong enough not be disrupted by random thermal motion. In practice, it is the bonds with the very strongest permanent dipoles that display this behaviour, and these are the ones that occur in molecules where a highly electronegative atom (oxygen or fluorine) is attached to hydrogen. Since hydrogen only has one electron, displacement of this electron towards the electronegative atom goes a long way towards generating a ‘naked proton’ which is wildly keen to get additional electron density from somewhere- anywhere. The intermolecular hydrogen bonds that are formed are longer than covalent bonds, but shorter than atoms in different molecules would normally approach one another, and they preserve direction just like covalent bonds. In substances held together by hydrogen bonding, such as liquid water, random thermal forces are not sufficient to reorient these molecules to break these bonds: instead, water molecules exchange one strong, directional hydrogen bond for another as they slide past one another.
Like dispersion forces, the strength of hydrogen-bonding can be estimated by looking at the energy required to vaporise a material.
In ethanol, C2H4OH, EVap = 44 kJ.mol–1
...slightly more than butane, which has a higher molecular weight but no hydrogen bonding.
![[Figure 1.6 and 1.7] –hydrogen bonding between water and ethanol; bond lengths marked on figure; O-H 85 pm, O...H 180 pm](ch1_p3_8.jpg)
In water, H2O, EVap = 41 kJ.mol–1
![[Figure 1.6 and 1.7] –hydrogen bonding between water and ethanol; bond lengths marked on figure; O-H 85 pm, O...H 180 pm](ch1_p3_9.jpg)
...only slightly less than ethanol, despite its much smaller molecular weight: this is because with two hydrogens and one oxygen, each water molecule can form one-and-a-half hydrogen bonds, rather than one.
The directionality and permanence of hydrogen bonds are important in maintaining the three-dimensional structure of large biological molecules such as proteins and DNA.
![[Classical figure of hydrogen bonds in base pairing of DNA]](figure.jpg)
Structure Determination by X-Ray Diffraction
We have talked about how molecules held together by covalent bonds have clearly defined structures, and how ionic solids have clearly defined lattice structures. In metallic solids as well, the nuclei are generally arranged in a regular lattice. But how do we know that these structures exist? And how do we know what they are? In chemistry we are not allowed to just make things up, we need some sort of experimental justification for what we say, and the supreme method for experimentally investigating structures in the solid state is X-ray diffraction.
We use X-rays because the wavelength of X-rays (0.01 to 10 nm) is similar to the distance between nuclei in solid materials. This means that when X-rays are scattered through these materials, they will be able to undergo constructive and destructive interference- diffraction- with the electrons present to generate a diffraction pattern, from which many months of arduous human effort or a few seconds of computer are typically needed to work back and find the three-dimensional pattern of electron density that created the diffraction pattern. Because the highest electron density arises from the core electrons, the diffraction pattern will be a function of the position of the nuclei. This also means that it will be insensitive to the positions of any hydrogens in the structure, so it is often impossible to accurately determine exactly where they will be using X-ray diffraction.
![[Diagram of how it works- not silly picture of machine as in textbook Figure 1.10!]](figure.jpg)
Recall the formulae for electromagnetic radiation:
ν = c/λ
Where
ν = frequency in s-1
c = the speed of light, 2.997 924 58 m.s-1
λ = wavelength in m
E = hν
Where h = Planck’s Constant, 6.626 068 76 × 10–34 J.s
The process of finding a structure from an X-ray diffraction pattern is not entirely straightforward. Usually an iterative process of refinement is used, where the diffraction pattern for an initial guess at the structure is calculated and then modified one atom at a time to make something that looks a little bit more like the experimental diffraction pattern until the calculated and experimental results are in some kind of agreement. For best results, we need a large single crystal of the substance we want to investigate- the more regular the structure of the object we are scattering from, the clearer our diffraction pattern will be. There are a number of traps for young players that we need to bear in mind when considering X-Ray structures.
- X-Ray diffraction tells us about the structure in the crystal: when a compound melts, or is dissolved in a solvent, and still more when it vaporises, it might have quite a different structure. In an extreme example, many membrane-bound proteins have a hydrophobic section crossing the cell membrane whose structure is largely imposed by the hydrophobic molecules in the membrane: should you somehow manage to crystallise one of these notoriously difficult-to-crystallise substances from a solvent that can solublilise both the hydrophobic and hydrophilic parts of the protein, you are likely to end up with a very different structure from the one the protein adopts in the cell.
- Molecules do not have a single, fixed structure. In general, molecules are continually flexing and bending; chemical bonds are like springs, not rods, and are continually stretching and compressing. In a structure it may be possible to freely rotate around many of the single bonds in the molecule. All these things mean that what we observe by X-Ray diffraction is a smeared-out average of all the possible molecular structures under the given conditions.
- As we said before, it can be difficult to figure out where the hydrogens are, so it is unwise to base your theory of everything on the position of hydrogens in your molecular structure. If there is a rapidly rotating group- a methyl group, for instance- it will also be difficult to pin down.
Where are the Bonds?
X-Ray diffraction shows us the position of the nuclei, not how they are bound together. As we have said, for ionic and metallic solids, there are no localised bonds; but if we are looking at a molecular compound held together by covalent bonds, we want to be able to tell which nucleus is bound to which and where one molecule ends and another begins. We do this in a rather crude way, like the mythical giant Procrustes, by setting a distance and saying that nuclei closer together than that distance are bound, while those further apart are not bound. We can then draw straight lines between the nuclei we have decided are attached to represent the bonds.
The distances we set are covalent radii, based on average bond distances in a large number of molecular compounds- usually determined in turn from X-ray diffraction data, but ultimately resting on bond lengths determined by rotational spectroscopy. For example, the covalent radius for carbon is 68 pm and the covalent radius for chlorine is 99 pm, so we would say there was a bond between carbon and chlorine if the nuclei seemed to be 167 pm apart in our structure. Actually, we would say there was a bond between carbon and chlorine if the nuclei seemed to be 200 pm apart in our structure, unless doing so would exceed the valency of carbon or chlorine. ‘Near enough is good enough’, as we used to say at NASA.
Using our Procrustean rule and keeping in mind the valency of the elements concerned, we can usually get a good result for organic molecules, which are well behaved. When we move on to inorganic molecules that may approach closer to ionic than covalent bonding, things can get very complicated.
![[Figure – well behaved organic molecule]](figure.jpg)
![[Figure – diborane- very naughty!!!]](figure.jpg)
Our Procrustean rules for diborane give a structure where each boron atom is bound to five other things (not three, as we would expect) and each hydrogen atom is bound to two things (not one, as we would expect). The current understanding of this structure is that the bonding between the two borons and the two hydrogens involves two equivalent delocalised molecular orbitals containing four electrons in total- thus, two electron pairs to give five ‘electron-deficient’ bonds. Remembering caveats #2 and #3 above, though, I would wager than an equally good description of bonding in diborane is given by a rapid interconversion of the two structures below.
![[Figure – Fellows diborane, behaving itself, of course, as you would guess from the name]](figure.jpg)
To conclude our discussion of bonding, I want to encourage you to think about molecules as things composed of nuclei and electrons, not atoms and bonds – all the different forms of bonding can be understood in terms of the competing repulsive and attractive forces between the positively charged nuclei and the negatively charged electrons, as described by Coulomb’s law. Fundamentally, there is no such thing as an atom.
Valence Shell Electron Pair Repulsion model
Having told you not to think about bonds and atoms, I am now going to talk about them, to refresh your memory about how Lewis structures can be transformed into a passable representation of the true three-dimensional structure using a few simple rules. Ultimately, Lewis structures are accounting devices based on the rules of valency and the results of experiments carried out in 250 mL beakers; and the true three-dimensional structures are determined experimentally using X-Ray Diffraction, Nuclear Magnetic Resonance Spectroscopy, or some combination of Infrared and Microwave Spectroscopy. So it is neat that there is such a simple model to connect the two!
The basic idea of the VSEPR model is this:
Electrons are suspicious mongrels and will stay as far away from each other as they possibly can.
(As you can see, this is just another way of stating Coulomb’s Law).
Consider the series of hydrides formed by combining the elements of the second row of the periodic table with hydrogen. The Lewis structures of these are shown on the right.
To predict the three-dimensional structure of these molecules, all we do is count the number of pairs of electrons around the central atom and assume that these pairs will arrange themselves so as to stay as far away from each other as possible- like charges repel.
- Lithium hydride can only form a linear molecule anyway, since there are only two atoms involved.
- In beryllium hydride, the two bonds stay as far away from each other as they can- a H-Be-H bond angle of 180° - so this molecule is linear too.
- In boron hydride, the three bonds will again stay maximally apart, so we expect a flat molecule pointing to the corners of an equilateral triangle- a trigonal planar molecule- with H-B-H bond angles of 120°.
- In methane, the four bonds can achieve maximum separation if they point to the corners of a tetrahedron. It is a tetrahedral molecule, with H-C-H bond angles of 109.5°.
- In ammonia we have a lone pair and three bonding pairs in the Lewis structure- the four electron pairs still try to maximise their separation, so the electronic geometry is tetrahedral. But the molecular geometry is a pyramid based on an equilateral triangle- a trigonal pyramidal structure- with H-N-H bond angles of approximately 109.5°. Experimentally, these bond angles are a bit less, about 107°, which can be rationalised by assuming that the electrons in bonding pairs are less repulsive than electrons in lone pairs because the bonding-pair electrons have to sit tight and behave themselves to form the bond, while the lone-pair electrons are more exuberant and can expand more freely into space.
- In water the electronic geometry is still tetrahedral, and the H-O-H bond angle is a bit less than 109.5° - about 104.5°, since there are two uninhibited repulsive lone-pairs. Water is a bent molecule.
- Finally, hydrogen fluoride is a linear molecule again. But its electronic geometry is tetrahedral.
The VSEPR model can also be applied to molecules with different substituents, and with multiple bonds. Where a multiple bond is present, it is considered to be a single ‘electron domain’. For example, in formic acid, HCOOH:
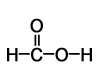
There are three separate regions of electron density attached to the central carbon, so this carbon is a trigonal planar centre, with H-C-O and O-C-O bond angles all about 120°.
Assigning bonds to X-ray structures was most straightforward for organic compounds, where bonding is essentially covalent and bonds can be clearly defined: the same is true for the VSEPR model. It gives the best predictions for organic compounds and other compounds composed of non-metals, and often falls down where the simple picture of all electrons in clearly defined bonds and lone-pairs does not apply. Some instances where VSEPR theory may lead you astray:
- Amines have a trigonal pyramidal structure, as predicted by VSEPR theory. But in amides there is interaction between the lone pair on nitrogen and the carbonyl carbon to give partial double-bond character to the C-N bond, and most amide nitrogens are trigonal planar.
- Despite having widely different numbers of electrons in the valence shell, numerous metal compounds from across the d-block with the formula ML6 have octahedral symmetry.
This makes sense when we consider that all the bonds shown in these structures are coordinate bonds, where both electrons in every bond come from a lone pair on an oxygen. Although the electrons d-orbitals nominally sit in the valence shell, they really have very little to do with the bonding. So applying our VSEPR theory to the actual bond pairs gives the octahedral structures we have drawn.


- The molecular fluorides of the group 2 metals are all predicted to be linear by VSEPR, but as we ascend the periodic table they become increasingly more bent.
| Experiment |
High-Level Quantum Theory [Seijo et al, J. Chem. Phys. 94. 3762, 1991) |
|

|
180o | 180o |

|
180o | 180o |

|
145o | 180o |

|
120o | 144o |

|
108o | 126o |
It would be cruel to stop there without offering some sort of explanation. You don’t have to read this explanation or learn it for the exam, it is just here because I like websites without any mysterious dead-ends. First of all, these are all unstable gaseous molecules with covalent bonds that are very weak indeed, so it is easy for the bonds to jiggle about: indeed, the calculations suggest that the dependence of molecular energy on bond angle is very weak for these compounds- almost zero for CaF2. So experimental measurements might be highly infected with the properties of excited states of these molecules that are see-sawing back and forth at a rate of knots. Secondly, the bending increases as the central metal becomes more polarisable, and we can explain this by extending our VSEPR theory in a hand-waving way to the highest core orbital. Both Sr and Ba have full d subshells immediately ‘below’ the valence shell- being polarisable means that they shift easily in response to other charges, so it makes sense that they will try to avoid the M-F bonds as much as they can, as well as trying to avoid each other. On the basis that lone-pair lone-pair interactions are more repulsive than bond-bond interactions, it is not surprising that we end up with a bent molecular structure.
The Ideal Gas
After the embarrassingly poor segue from X-ray diffraction to VSEPR theory, I am kind of ashamed to do the same thing again- but we’ve just been talking about the properties of alkaline earth fluorides in the gas phase, so what better time to review the properties of gases in general?
At a fixed temperature, the pressure of a gas is inversely proportional to its volume. If we halve the volume, we double the pressure. This is sometimes called Boyle’s Law.
| p ∝ | 1 |
| V |
Likewise, at a fixed volume, the pressure of a gas is directly proportional to its temperature. If we double the absolute temperature- an increase, say, from 298 K to 596 K – we double the pressure. This is often called Charles’ Law.
p ∝ T
And if we take two gases at the same pressure and temperature, then the volumes are proportional to the number of moles of gas present. One mole of gas will occupy half the volume of two moles of gas, so long as pressure and temperature are kept the same. This is known as Avogadro’s Law.
V ∝ n
And, there is one other law, the law of Gay-Lussac, which says that at a constant pressure the volume of a gas is directly proportional to the absolute temperature.
V ∝ T
But there is no need for us to remember all these separate laws with their peculiar names, since they can be bundled together into one expression, the ideal gas law:
pV = nRT
R here is the ideal gas constant, which if we express all the other quantities in SI units has the value 8.314472 J.K-1.mol-1. If this is not a value that you have already committed to memory, I suggest you do so now. The SI units we use are:
The physical basis for the ideal gas law is that a gas is mostly empty space, and the remainder is tiny tiny particles zipping around at considerable velocities. What we perceive as temperature is a measure of how fast these particles are moving- their kinetic energy- and it is these particles hitting the sides of whatever is constraining them and bouncing off again that exerts pressure. If you keep this physical picture clearly in your mind, you are not likely to go wrong with remembering and using the ideal gas law.
Provided pressure is relatively low, the volume of space occupied by the actual molecules of a gas is low and the effect of any attractive or repulsive forces between the gas molecules is minimal, so the ideal gas law is a good model for gas behaviour. As we move towards denser and denser gases with stronger and stronger intermolecular interactions, we need to make modifications to our theory to make it more complicated, and then throw it away all together. But there are plenty of fun things we can do with it if we keep its limitations in mind. A gas that obeys the ideal gas law is called (suprise) an ideal gas. All gases that really exist will deviate to some extent from full obedience to the law, and are called non-ideal.
Using the Ideal Gas Equation
Example 1
Calculate the volume occupied by one mole of gas at atmospheric pressure (1 atmosphere, atm = 1.013 × 105 N.m-2) and 0 oC.
pV = nRT
We are asked to find volume, so we rearrange the expression like so:
| V = | nRT |
| P |
And put in our values:
| V = | 1 mol × 8.314 N.m.K-1.mol-1 × 273.15 K |
| 1.013 × 105 N.m-2 |
| V = | 1 mol × 8.314 N.m.K-1.mol-1 × 273.15 K |
| 1.013 × 105 N.m-2 |
V = 0.02242 m3
Example 2
At 0oC, a cannister of gas is pressurised to 2.0 × 105 N.m-2. What will the pressure rise to if it is heated to 40 oC?
pV = nRT
We shift all the things that are kept constant in this question to one side, and all the things that are changing to the other side.
| p | = | nR |
| T | V |
Since nR/V is a constant, p/T must remain the same for all possible values of p and T, so we can write:
| p1 | = | p2 |
| T1 | T2 |
And rearrange to solve for the one thing we don’t know:
| P2 = p1 × | T2 |
| T1 |
| P2 = p1 × | T2 |
| T1 |
| P2 = 2.0 × 105 N.m-2 × | 313.15 K |
| 273.15 K |
P2 = 2.3 × 105 N.m-2
Example 3
6.0 g of an unknown substance is placed in a sealed 1 L vessel, the vessel is heated to 1400 oC and the substance vaporises. If the pressure in the vessel is measured to be 1.21 × 107 Pa, what is the molecular weight of the unknown substance?
I’ve put the pressure much higher than atmospheric pressure, so we can ignore the contribution from the gas that was there to start with. We need to solve for n, the amount of substance in moles.
pV = nRT
| n = | pV |
| RT |
| n = | 1.21 × 107 N.m-2 × 1.0 × 10-3 m3 |
| 8.314 N.m.K-1.mol-1 × 673.15 K |
n = 0.870 mol
So we can now find the molecular weight of the substance-
| M = | 6.0 g | = 6.9 g.mol-1 |
| 0.870 mol |
Mixtures of Ideal Gases
Since the ideal gas equation refers to the case where there are no appreciable forces between the gas molecules, it can be applied to mixtures of gases independently. If we have a certain volume containing n1 moles of gas one and n2 moles of gas two, then:
pV = (n1 + n2) RT
And we can define partial pressures p1 and p2 such that:
p1V = n1RT
p2V = n2RT
and:
p = p1 + p2
A useful term when discussing the properties of mixtures is the mole fraction, x- for a particular substance, this is the fraction of the total moles present that are that substance.
| x1 = | n1 |
| n |
If the mixture is a mixture of ideal gases, this is related in an incredibly straightforward way to partial pressure:
| x1 = | p1 |
| p |
Example
The pressure outside my office is about 8.98 × 104 N.m-2. The mole fraction of nitrogen in the atmosphere is about 0.78. What is the partial pressure of N2 in my office?
| XN2 = | pN2 |
| p |
pN2 = p × xN2
pN2 = 8.98 × 104 N.m-2 × 0.78
pN2 = 7.0 × 104 N.m-2
Now let’s say I sealed all the doors and windows of my office, put 2.0 kg of liquid nitrogen inside, and let it vaporise. What will be the resulting partial pressure of N2 in my office, and the corresponding mole fraction? (Of course, I have to tell you how big my office is so you can answer this question. Let us say it is about 6 × 4 × 3 metres.)
pV = nRT
| pextra = nextra | RT |
| V |
(Hang on, I have to look up the temperature for you as well - it seems to be about 18 oC)
V = 6 m × 4 m × 3 m = 72 m3
| nextra = | 1000 g | = 36 mol |
| 28 g.mol-1 |
| pextra = | 36 mol × 8.314 × 8.314 N.m.K-1.mol-1 × 291 K |
| 72 m3 |
pextra = 1.2 × 103 N.m-2
So the final p N2 will be 7.1 × 104 N.m-2 ...nothing much to worry about, I am thinking.
Molecular Energy Levels
I have said that temperature is a measure of the kinetic energy of particles in a gas, and now I will tell you exactly how the two are connected. There is an equation which makes this fundamental connection that will come up again and again in physical chemistry: it can in fact be considered a definition of temperature, and is called Boltzmann’s Law.
In a gas, particles will be moving around randomly at different velocities (vi) and therefore at different kinetic energies (εi, = ½mvi2). It is possible to derive using fairly elementary statistics an expression for how the number of particles with a particular energy (Ni) depends on the temperature.
| Ni ∝ e | -εi |
| kBT | |
Where kB, Boltzmann’s constant, is just the ideal gas constant divided by Avogadro’s number.
R = kB × NA
You can see that Boltzmann’s constant is a more fundamental constant than the ideal gas constant, and also that it is just an artifact of our measuring system. If our units for energy and temperature were different, kB would be 1 and all our equations would be simpler!
We can get rid of the proportionality and write:
| = |
|
This is a law that is derived from statistics, and is not specific to the kinetic energies of particles in a gas. It is applicable to all sorts of energies, and all sorts of systems. That is why it keeps cropping up in physical chemistry.
In a gas, the distribution of energies is essentially continuous: there is a smooth curve of possible energies, and to as accurately as we can measure (and a good deal more) there will be plenty of particles at every possible kinetic energy value anywhere near the average, so there is never much need for calculating specific values of Ni; instead, we use Boltzmann’s law to calculate average kinetic energy values.
For other systems of interest in physical chemistry, the distribution of energies is not at all continuous. Instead, it is quantised. Quantised, quantitative, quantum- these are terms that the rest of this unit will be gleefully larded with. Take, for example, the vibration of a chemical bond. For most typical chemical bonds, there will only be two possible energies at room temperature: the ground state, with a population N0, and the first excited state, with a population N1.
Using Boltzmann’s law, we can determine the relative number of molecules in each state, N1/N0, if we know the energy difference between them:
| Ni ∝ e | -ε1 |
| kBT | |
So,
| N1 | = |
| |||||
| N0 |
|
| N1 | = |
| ||||||
| N0 |
| N1 | = |
| ||||||
| N0 |
It is the form of Boltzmann’s law in the last line that is most generally useful, and well worth committing to memory. A rough measure of the background thermal energy at a temperature T is kBT : if energy levels are separated by much less than this, quantisation is not usually important and we are better off considering an average energy; if energy levels are separated by much more than this, we definitely have to use the quantum mechanical model to understand the system.
We will look properly into how and why this quantisation of energy levels arises later in the unit, but for the moment we may as well introduce a few factoids about energy levels.
Translational energy levels are associated with the movement of particles through space. As we have said with reference to the behaviour of a gas, they are very closely spaced, and we can only observe effects associated with translational quantisation at extremely low temperatures.
Rotational energy levels are associated with the rotation of molecules. They are much further apart than translational energy levels, but can be experimentally separated, so that typical gas molecules at room temperature will populate dozens of rotational levels in significant numbers.
Vibrational energy levels are much further apart again, so that at room temperature, most molecules are in their lowest vibrational state.
Electronic energy levels are even further apart, which is why chemistry is possible. At higher temperatures where energies are such that electrons keep flying up into excited states all the time (e.g., in the sun), there is little scope for chemical bonding and all the amazing fun that arises from it.
Questions with worked answers
Question 1.1
The energy released by the complete combustion of gaseous methane to CO(g) and H2O(g) is 803 kJ.mol-1.
Given that:
- The O-O bond energy is 498 kJ.mol-1
- The C-O bond energy in CO2 is 805 kJ.mol-1
- The O-H bond energy in H2O is 497 kJ.mol-1
Estimate the C-H bond energy in methane.
Hint: Write a balanced chemical equation for the combustion of methane and then think about the number and type of bonds broken or made as the reaction proceeds.

